Dalla sezione aurea ai frattali
Consapevolezza

Consapevolezza
Dalla proporzione aurea studiata nell’antica Grecia alle geometrie frattali rivelate dall’informatica moderna, la matematica ha progressivamente svelato l’ordine nascosto nella natura.
Spirali, galassie, polmoni, architetture e opere d’arte sembrano rispondere a schemi ricorrenti che collegano microcosmo e macrocosmo.
Un percorso che unisce rigore scientifico e interrogativi filosofici sulla struttura profonda della realtà.
Varutti Guerrino
Origine della sezione aurea
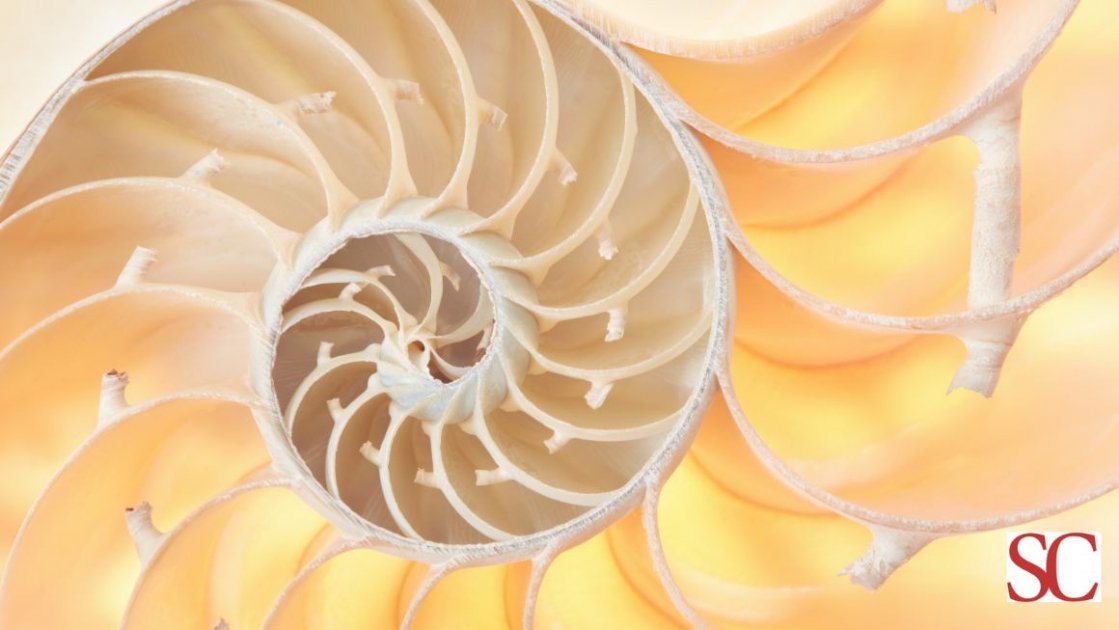
La distribuzione dei petali in una rosa, l’armoniosa spirale di alcune conchiglie e quella dell’intera galassia, e il celeberrimo Partenone di Atene sono tutti legati dallo stesso meraviglioso numero irrazionale, “φ”.
Non esprimibile con una frazione, caratterizzato da una serie infinita di numeri decimali che si ripetono in maniera apparentemente casuale “1,6180…”, indicato fin dall’antichità appunto con la lettera greca “φ”, ha una proprietà particolare che affascina gli studiosi e gli artisti da migliaia di anni. Il rapporto proporzionale dal quale deriva, ha la misteriosa proprietà di imprimere un senso di bellezza e armonia a qualsiasi cosa che la natura esprima. Proprio per questo motivo fin dal tempo di Pitagora è stato definito “divina proporzione” e poi, nel Rinascimento, fu chiamata “sezione aurea”.
La cosa affascinante, meravigliosa e misteriosa che sta dietro la sezione aurea è appunto come un numero irrazionale e infinito, riesca a generare bellezza e armonia che sono sempre accompagnate invece dal concetto di definito e proporzionato.
Dal punto di vista prettamente matematico, la sezione aurea è quella parte di segmento media proporzionale tra il segmento intero e la parte rimanente. Si tratta quindi di un rapporto tra due grandezze geometriche. Interessante è come le varie caratteristiche del numero aureo siano state oggetto di attenzione da parte di studiosi, filosofi e artisti nei contesti storico-culturali più diversi.
Un po' di storia
La prima definizione scritta del rapporto aureo risale all’età ellenistica: la ritroviamo infatti nel VI libro degli Elementi di Euclide. Della biografia di Euclide ci è noto pochissimo: visse ad Alessandria tra il IV e il III secolo a.C., studiò matematica ad Atene sotto la guida di filosofi platonici e compose tredici trattati su vari argomenti scientifici (Ottica, Dati, Fenomeni, Divisione di figure, ecc…).
Il rapporto aureo è da lui definito come «proporzione estrema e media» e la nomina relativamente alle aree e alla costruzione del pentagono, dell’icosaedro e del dodecaedro regolare.
In età greca, inoltre, φ è utilizzato per la costruzione di numerose figure geometriche quali i poliedri platonici e la stella pitagorica, ma soprattutto come principio di armonia. Si pensava infatti che il rapporto aureo stesse alla base della perfetta struttura del corpo umano (volto, busto, figura intera stavano tra loro in proporzione aurea); da questo principio vennero elaborati i canoni scultorei da cui deriva in parte lo stesso concetto di bellezza e proporzione classica.
In campo architettonico, anche lo stesso Partenone fu progettato da Fidia sfruttando il numero aureo, facendo sì che l’imponente costruzione non risultasse tozza e sgraziata, ma anzi proporzionata e perfetta.
Il ruolo nella scienza della sezione aurea
Importante campo interessato al numero aureo fu quello della scienza. Keplero sentì la necessità di trovare un nesso tra le distanze planetarie e il numero aureo. La sua profonda fede religiosa infatti, lo portò a pensare che l’universo, nei suoi rapporti tra i pianeti, dovesse chiaramente rispecchiare il suo creatore: le stelle, il sole e le loro distanze erano dunque metafora delle tre persone divine, Padre, Figlio e Spirito Santo. Se, come lui stesso afferma, “Dio geometrizza sempre”, sicuramente bisognava ricorrere a enti geometrici legati al rapporto aureo per calcolare le orbite dei pianeti. Assistiamo così a una connessione di φ all’azione divina proprio per le sue caratteristiche.
Nel “Mysterium Cosmographicum” del 1597 Keplero ipotizzò la teoria che legava le orbite dei pianeti, rappresentate come sfere di varie dimensioni, ai poliedri regolari platonici, che venivano in esse inscritti e circoscritti. Il rapporto tra i raggi delle varie sfere doveva corrispondere al rapporto tra le varie orbite dei pianeti. Tutto questo schema di proporzionalità era stato strutturato a partire dalla sfera della terra, quale misura di tutte le altre orbite: fungeva infatti da spartiacque tra i solidi in equilibrio stabile (cubo, tetraedro e dodecaedro) e quelli in equilibrio fluttuante (ottaedro e icosaedro).
L’utilizzo dei poliedri regolari inscritti e circoscritti rispecchia proprio il tentativo di concepire la struttura dell’universo in chiave matematica e quindi sotto un profilo armonico e proporzionato. La scoperta di altri due nuovi pianeti oltre l’orbita di Saturno, Urano e Nettuno, invalidò completamente il modello di Keplero, tuttavia egli fece compiere un enorme passo avanti al metodo scientifico-astronomico: si impegnò infatti a unire i dati sperimentalmente ottenuti a un modello matematico organizzato.
Nel Medioevo, Arnolfo di Cambio, per progettare il Palazzo Pubblico di Firenze, noto come Palazzo Vecchio, tenne conto del rapporto aureo. Piero della Francesca, nella flagellazione di Urbino, inquadra la scena in una prospettiva matematica basata sulla sezione aurea: nel Rinascimento italiano infatti, la ricerca di prospettiva scientifica è spesso accompagnata dall’impiego della sezione aurea (la ritroviamo anche in Leonardo da Vinci).
Oltre a essere utilizzato nei più svariati modi, il rapporto aureo è stato anche riscontrato nella struttura di molti elementi naturali. I petali della rosa, per esempio, formano con la loro inclinazione, angoli al centro, che danno, in rapporto con l’angolo giro, un numero che ci avvicina sempre più a φ man mano che aumenta l’ampiezza angolare.
Nei cosiddetti alberi aurei, i rami lungo il tronco e le foglie lungo i rami, si distribuiscono secondo un preciso schema a spirale, detto fillotassi: il rapporto tra il numero di foglie e quello dei giri da esse compiuti lungo il ramo si avvicina al numero aureo all’aumentare dei valori numerici. Inoltre la nostra stessa galassia e molte conchiglie hanno la forma di una spirale logaritmica, cioè basata su rettangoli aurei (rapporto tra base e altezza è pari a φ) sempre più piccoli.
Innumerevoli sono i casi in cui φ, questo numero magico e misterioso, ha affascinato e continuerà ad affascinare l’uomo per la sua inspiegabile proprietà di far scaturire bellezza e proporzione.
Rapporto aureo e la serie di Fibonacci
Lo studio della spirale e del rapporto aureo fu eseguito da un matematico di nome Leonardo Fibonacci verso il 1170 il quale con una spiegazione matematica di carattere mercantile e monetario propose il cosiddetto “problema dei conigli”, dal quale scaturì una successione numerica chiamata “serie di fibonacci” ed è ricostruibile in base ad una semplice relazione: ogni numero è dato dalla somma dei due che la precedono. Osservando la successione delle potenze di si scopre che è la Serie di Fibonacci anche la seguente ȹ0, ȹ1, ȹ2, ȹ3, ȹ4, ȹ5, ȹ6, ȹ7.
Nel 1494 il geniale Luca Pacioli pubblicò l’opera chiamata “De divina proportione, e in questo libro riprende il concetto della sezione aurea della matematica antica, applicando ai criteri estetici delle arti figurative ed in particolare alle proporzioni del corpo umano.
Origine della geometria frattale
Verso la fine del XIX secolo, nel 1875, il matematico tedesco C. Weierstrass descrisse una curva con caratteristiche decisamente strane, considerate addirittura patologiche e sgradevoli dai suoi colleghi, in quanto mettevano in discussione i concetti di distanza, di area, di spazio e di dimensione. Altri, come il tedesco G. Cantor e il polacco W. Sierpinski, ottennero linee e figure geometriche di cui non si riusciva a calcolare la lunghezza e l'area e nel 1890 l'italiano G. Peano dimostrò che una curva continua priva di superficie può riempire una regione dello spazio.
Un giovane matematico francese di nome G. Julia ha pubblicato una relazione sul suo lavoro con le funzioni iterate. La sua era una equazione relativamente semplice, che faceva soltanto uso di moltiplicazione e addizione ripetute ad infinitum. Per farsi effettivamente un’idea dell’immagine codificata nella sua formula matematica, Julia avrebbe dovuto risolvere milioni di iterazioni di tale formula, processo che gli avrebbe richiesto decenni. Perciò pur avendo concepito un frattale in termini matematici, egli non ne vide mai veramente uno.
Le profonde implicazioni della formula di Julia furono rivelate soltanto nel 1975, quando la sua equazione venne risolta con l’aiuto del computer.
B. B. Mandelbrot
B. B. Mandelbrot, un matematico franco-americano asseriva: “Perché spesso la geometria viene descritta come fredda e arida? Un motivo è la sua incapacità di descrivere la forma di una nuvola, di una montagna, di una costa o di un albero. Le nuvole non sono sfere, le montagne non sono coni, le coste non sono circoli e gli argini non sono regolari, nemmeno la luce viaggia secondo una linea retta... La natura non rivela semplicemente un grado più alto ma un livello del tutto diverso di complessità.”
B. B. Mandelbrot, che analizzò i modelli nei sistemi caotici in un laboratorio informatico dell’IBM, fu il primo a osservare quello che Julia aveva solo potuto immaginare. B.B. Mandelbrot fu colto da timore referenziale delle superbe immagini organiche e infinitamente complesse generate dalle formule frattali. Egli fu il primo a osservare che le immagini frattali possedevano ripetuti modelli auto similari, indipendentemente dalla scala su cui esse erano esaminate, quanto più egli ingrandiva le immagini, tanto più la struttura si rivelava essere la stessa.
Intrinseca alla caotica complessità delle immagini frattali è la presenza di modelli che si ripetono eternamente, annidati gli uni con gli altri. Il giocattolo internazionalmente noto, le bambole russe dipinte a mano che si annidano l’una nell’altra, fornisce un’idea approssimativa della natura delle immagini ripetitive di un frattale.
Ogni versione più piccola della bambola, è simile alla bambola, più grande dentro cui è annidata, ma senza doverne essere per forza una esatta replica. B.B. Mandelbrot introdusse il termine auto similare per descrivere gli oggetti del genere che osservò nella nuova matematica, che egli chiamò geometria frattale. Nella complessità delle sue immagini frattali osservò modelli realistici che assomigliavano a forme comuni in Natura, come insetti, conchiglie e alberi.
Storicamente la scienza aveva spesso documentato la presenza di modelli organizzativi auto similari su diverse scale di struttura della Natura, tuttavia, prima che B.B. Mandelbrot introducesse la geometria frattale, questi modelli auto similari erano ritenuti semplicemente curiose coincidenze dai razionali e dai deterministi.
Modelli auto similari si ritrovano in tutta la Natura e specialmente nella struttura del corpo umano. Per esempio nel polmone umano lo schema delle ramificazioni lungo i passaggi per l’aria costituiti dal grande bronco è ripetuto nella struttura ramificata dei bronchi più piccoli e degli ancor più piccoli bronchioli.
Anche le arterie del sistema circolatorio, come la rete corporea dei nervi periferici, esibiscono modelli ramificati ripetitivi, auto similari.
Dato che la geometria frattale è effettivamente il principio del disegno della Natura, la biosfera rivela intrinsecamente modelli auto similari annidati ad ogni livello della sua organizzazione.
Aspetti filosofici della Geometria Frattale
La geometria frattale non è solo una branca della matematica, ma porta con sé profonde implicazioni filosofiche che riguardano la natura della realtà, la percezione, il determinismo e il caos. Ecco alcuni dei suoi principali aspetti filosofici:
- I frattali mostrano come strutture infinitamente complesse possano essere contenute in uno spazio finito. Ad esempio, il Set di Mandelbrot ha dettagli sempre nuovi indipendentemente da quanto si ingrandisca, suggerendo che l’infinito sia presente in ogni livello della realtà. Questo solleva domande sulla natura dell'infinito. È un concetto puramente astratto o una proprietà intrinseca dell'universo? La realtà è costruita su livelli di dettaglio infiniti?
- I frattali mostrano autosimilarità, ovvero la stessa struttura ripetuta a diverse scale. Questo principio ricorda il concetto olografico, secondo cui ogni parte dell'universo potrebbe contenere informazioni sul tutto. Il nostro universo potrebbe essere strutturato in modo frattale? Se ogni parte contiene informazioni sul tutto, ciò potrebbe implicare una connessione profonda tra microcosmo e macrocosmo, tra individuo e universo.
- Molti frattali emergono da equazioni semplici ma iterative, dimostrando che il caos apparente può nascere da regole rigorose. Questo richiama la teoria del caos, che mostra come piccoli cambiamenti nelle condizioni iniziali possano generare esiti imprevedibili (Effetto Farfalla).
Il mondo è governato dal caso o da leggi matematiche nascoste? Esiste un ordine sottostante al caos apparente?
Molte strutture naturali (alberi, polmoni, fiumi, montagne) seguono schemi frattali, suggerendo che la geometria frattale sia una "firma" della natura. Questo porta a ipotizzare che l’universo stesso possa essere di natura frattale. Se la realtà segue schemi frattali, significa che è costruita secondo un ordine profondo? Esistono leggi universali che regolano tutto ciò che esiste, dall’atomo alla galassia?
Nei frattali, l'osservatore gioca un ruolo chiave: la loro complessità appare solo quando vengono analizzati in profondità. Questo richiama il problema filosofico della percezione nella meccanica quantistica: la realtà esiste indipendentemente dall’osservatore o viene "creata" nell’atto di osservarla?
Se i frattali dipendono dall’atto di osservarli, è possibile che la realtà stessa sia influenzata dalla nostra percezione? L’universo si costruisce man mano che lo esploriamo?
Molte tradizioni filosofiche e spirituali vedono nel concetto di autosimilarità un parallelo con l’idea di interconnessione universale. In alcune filosofie orientali, l’idea che il microcosmo rifletta il macrocosmo è un principio cardine (es. "Come in alto, così in basso").
I frattali potrebbero essere la manifestazione geometrica di principi metafisici? Se tutto è interconnesso su più livelli, significa che esiste un "disegno" nell’universo?