L'impronta dell'entropia nella fisiologia umana - prima parte

Scienza e Fisica Quantistica

Scienza e Fisica Quantistica

156 condivisioni

La seconda legge della termodinamica conferma la sua trasversalità in tutto l’Universo fisico. L’impronta dell’entropia è riconoscibile anche nell’ambito della fisiologia umana quando nell’organismo, o in sue parti, intervengono modificazioni a seguito di interazioni con l’ambiente esterno.

Il rapporto stimolo – risposta

Gli organi di senso rappresentano la base biologica della percezione. Nell’uomo completano la loro maturazione entro i primi 4-5 mesi di vita e la loro funzione è quella di registrare i cambiamenti che avvengono nell’ambiente e trasmetterli al cervello.

Per esempio il sistema visivo è sensibile alla luce emessa o riflessa da un oggetto (energia elettromagnetica) e i diversi sistemi sensoriali la traducono in impulsi nervosi.

Lo stesso dicasi per i suoni percepiti dal nostro apparato uditivo.

Ogni organo di senso comporta una trasduzione, ossia la modificazione di un tipo di energia presente nell’ambiente (ad esempio onde luminose o sonore) in segnali neuronali, ossia un altro tipo di energia.

Inoltre i sensi non rispondono solo alla stimolazione di una particolare forma di energia, ma devono anche fornire percezioni differenziate a fronte di eventuali variazioni del segnale esterno.

In sostanza ogni forma di energia può variare secondo due modalità: quantitativa e qualitativa.

Nella fase di registrazione i nostri organi di senso, come tutti gli strumenti di misura, sono però vincolati da alcuni limiti.

Il primo è legato al fatto che ogni sistema è sensibile solo ad un particolare tipo di energia.

Ciò comporta che molti altri stimoli possono essere presenti nell’ambiente ma noi non possiamo avvertirli, perché il nostro sistema sensoriale non è capace di rilevarli (1), almeno non in tempo reale. Di  questo problema me ne occuperò nell’ultima parte.

Un altro limite è rappresentato dall’intensità dello stimolo.

Questo vuol dire che qualsiasi stimolo fisico deve raggiungere un livello minimo per suscitare una sensazione. Tale livello, chiamato soglia assoluta, segna il confine fra gli stimoli che vengono recepiti dall’organismo (stimoli sovraliminari) e gli stimoli che, pur essendo presenti, non sono avvertiti dall’organismo (stimoli infraliminari) [1].

Un importante contributo in questo ambito venne dallo studio della fisiologia dell’occhio. Infatti si può dimostrare che l’occhio umano reagisce alla sensazione della luce in modo logaritmico. Per dare un idea, proviamo a immaginarci dentro una stanza completamente buia, e supponiamo di cominciare ad accendere una lampadina. La prima sensazione che proveremo sarà quella di essere quasi abbagliati da questa luce. Supponiamo adesso di accendere una seconda lampadina di uguale intensità. Adesso non percepiremo più questo secondo evento con una sensazione di abbaglio, ma semplicemente vedremo la stanza più luminosa. All’accensione di una terza lampadina la sensazione di abbaglio sarà sempre meno intensa e così via.

Altro esempio lo possiamo formulare pensando all’udito. Quando siamo fermi ad un semaforo per aspettare il verde e ad un tratto sentiamo il suono di un clacson lo avvertiamo in maniera molto netta provocandoci una sensazione molto intensa. Se a questo primo si aggiunge un secondo clacson non percepiremo una sensazione di intensità doppia rispetto alla precedente.

Un altro caso di relazione esistente tra stimolo e percezione può essere realizzato con un esperimento consistente nell'incrementare, di una certa quantità, il peso di un oggetto sostenuto da una persona. La percezione di tale stimolo (l'incremento di peso) risulta essere tanto meno accentuata, quanto più pesante è l'oggetto: ad esempio aggiungere 1 kg ad un oggetto il cui peso è di 50 g risulta essere percepito in maniera più gravosa rispetto ad aggiungere 1 kg ad un oggetto il cui peso iniziale è di 20 kg. In altri termini aumenti graduali e costanti del peso fisico si accompagnano ad aumenti via via sempre più deboli della sensazione di pesantezza.

La differenza appena percepibile pare sia una costante, che ha un valore specifico per ogni modalità sensoriale e misura l'intensità di uno stimolo dicendoci di quanto esso deve variare per essere percepito come diverso da un altro (Legge di Weber-Fechner).

Tornando all’esempio delle lampadine, nella rappresentazione grafica che mette in relazione lo stimolo con la risposta (v. fig.1), all’inizio ci sarà un plateau dovuto all’assenza di luce o comunque alla presenza di stimoli talmente deboli da essere al di sotto della soglia percettiva (stimoli infraliminari). Via via che il numero di lampadine aumenta ci sarà un incremento della percezione della luce che poi si trasformerà ancora in un plateau con una lenta crescita quando il numero delle sorgenti accese sarà sufficientemente elevato per cui l’occhio non sarà più in grado di apprezzarne la differenza. Quindi la curva sarà costituita da una soglia iniziale, seguita da un andamento di crescita approssimativamente lineare e quindi da una saturazione:

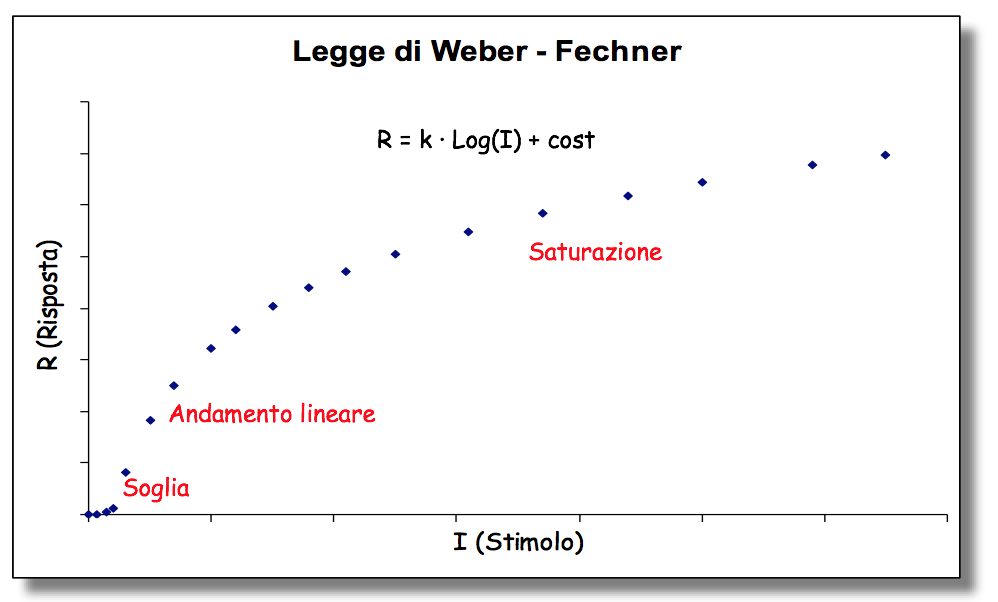
fig. 1 

Volendo semplificare, diremo che la risposta degli organi di senso presenta una curva con un andamento logaritmico, per cui noi possiamo descrivere la “sensazione” (risposta) come una costante (k) che moltiplica il logaritmo della “Intensità del segnale” (stimolo), più una costante che è dipendente dalla soglia:

R = k ·ln I + costante                       (1)

Entropia e statistica

In fisica esiste una grandezza che quando viene nominata incute soggezione e allo stesso tempo suscita fascino: l’entropia. A livello microscopico, tutte le leggi fisiche sono stranamente reversibili nel tempo, tuttavia a livello macroscopico, quando viene coinvolto un numero elevato di particelle, il tempo presenta una freccia ben definita: l’inchiostro versato in un bicchiere contenente acqua si diffonderà e si mescolerà, non si separerà mai dalla soluzione acquosa per tornare nel contagocce, quest’ultima sequenza è contraria al nostro senso del tempo.

L’uomo che diede un significato a tutto ciò fu Ludwig Boltzmann il quale, non preso molto sul serio dai suoi contemporanei, oggi viene considerato uno dei geni della fisica. Nella seconda metà del XIX secolo, intuì per primo che l’entropia, una grandezza già nota in fisica, in particolare nel secondo principio della termodinamica, era una misura del disordine di un sistema.

In particolare propose che fosse da mettere in relazione con il numero dei diversi modi microscopici (microstati) attraverso i quali si può ottenere una situazione osservabile sul piano macroscopico (macrostato) (2).

Un microstato di un sistema termodinamico rappresenta una precisa configurazione dei suoi parametri microscopici (per esempio masse, posizioni e velocità di tutte le molecole che costituiscono il sistema). Un macrostato rappresenta invece una condizione con valori ben determinati di pressione, volume e temperatura, tutte grandezze macroscopiche.

Inoltre, mentre ad ogni microstato possiamo associare uno ed un solo macrostato, ad ogni macrostato possono corrispondere più microstati possibili.

Pensiamo ad esempio alle molecole di un gas che, occupando il medesimo volume, possono avere velocità e posizioni molto diverse pur mantenendo la stessa energia cinetica media e quindi la stessa temperatura misurabile a livello macroscopico con un termometro.

Il risultato fondamentale a cui giunse Boltzmann fu che l’entropia S può essere calcolata, a meno di una costante, con un’espressione logaritmica del tipo:

S = k ·ln W + costante          (2)

in cui W rappresenta il numero di possibili modi equivalenti su scala microscopica (microstati) in cui le molecole possono essere organizzate fra loro per dare lo stesso stato macroscopico (macrostato) [2].

Boltzmann riuscì a trovare il legame tra il concetto termodinamico di entropia e quello di disordine passando attraverso una chiave di lettura statistica: qualsiasi situazione definita in modo tale da poter essere descritta in pochi modi diversi viene riconosciuta come ordinata e meno probabile. Al contrario, una qualsiasi situazione che possa essere descritta in molti modi, tutti equivalenti, viene detta disordinata e più probabile.

Quando nel secondo principio della termodinamica si afferma che l’entropia totale dell’Universo è in continuo aumento arriviamo a uno dei concetti più importanti di tutta la scienza: in un qualsiasi processo reale e spontaneo il disordine dell’Universo aumenta sempre. Anche se il moto di ogni singola particella è reversibile nel tempo, non lo è la tendenza verso l’aumento del “disordine” di una grande collezione di particelle. In questo consiste la freccia del tempo, ossia nel divenire macroscopico dell’Universo da uno stato di maggiore ordine, e meno probabile, ad uno di maggiore disordine, e più probabile, proprio come nel caso dell’inchiostro nell’acqua.

Tentiamo una sintesi

Alla luce di quanto sopra esposto, viene spontaneo tentare una sintesi accattivante. Nelle varie trasformazioni energetiche che avvengono nell’Universo, l’energia totale rimane sempre costante (Primo principio della termodinamica) anche se la sua qualità subisce una sorta di degrado a causa dell’inevitabile tendenza al disordine. In altri termini, ad ogni passaggio successivo, è come se l’energia perdesse di qualità e diventasse sempre meno disponibile per produrre lavoro.

In tutto ciò la somiglianza tra la legge sperimentale di Weber – Fechner (1) e l’interpretazione statistica dell’entropia fornita da Boltzmann (2) è sorprendente.

Gli accostamenti, ad esempio, tra la risposta a uno stimolo e l’entropia, così come tra il numero di microstati possibili e l’intensità dello stimolo stesso non possono passare inosservati: uno stimolo esterno sarà tanto più significativo quanto maggiore sarà il numero di microstati che metterà a disposizione del sistema e, allo stesso tempo, la risposta fisiologica sarà proporzionale al grado di disordine che viene introdotto a livello biologico a fronte di tale interazione con l’ambiente. Di fatto l’energia che viene fornita a livello cellulare genera un disordine in grado di produrre sensazioni e percezioni con una risposta che in linguaggio matematico diremo logaritmica.

Il nostro sistema percettivo, nel momento della trasduzione, trasforma energia ordinata ad esempio sotto forma di onde elettromagnetiche o acustiche, le quali contengono informazioni sull’universo circostante, in impulsi nervosi, l’unico linguaggio che il cervello è in grado di comprendere, anche se più disordinati. Questo connotato degenerativo comporta, dopo la trasduzione del nostro cervello, una perdita delle informazioni originali dello stimolo e impedisce un’ulteriore possibilità di produrre lavoro.

156 condivisioni